L’objectif de cette page est de présenter les définitions des termes techniques relatifs aux domaines de l’acoustique et de la vibration.
Elle s’adresse à toutes personnes souhaitant approfondir leurs connaissances en acoustique et en vibration.
Cette page est en perpétuelle évolution donc n’hésitez pas à nous contacter si vous avez des questions ou des remarques!
Les définitions sont positionnées de manière pédagogique comme pour un cours, donc normalement du plus simples au plus détaillés.
Nous accordons aussi beaucoup d’importance aux références car ce sont grâce aux personnes qui écrivent les livres, thèses et autres publications que nous pouvons réaliser ce travail de pédagogie. Par conséquent, nous nous efforçons à préciser au mieux nos références mais s’il en manque n’hésitez pas à nous en faire part.
L’acoustique est la science du son, ce qui inclut sa production, son contrôle, sa transmission, sa réception et ses effets. Elle concerne principalement l’étude d’onde et est donc considérée comme une branche de la mécanique.
Une vibration est un mouvement d’oscillation mécanique autour d’une position d’équilibre stable ou d’une trajectoire moyenne. La vibration d’un système peut être libre ou forcée.
Il s’agit de la variation de pression autour de la pression atmosphérique.
La pression sonore en échelle linéaire étant difficilement représentable (de 20μPa à 10Pa environ), le niveau sonore est quantifié suivant une échelle logarithmique.
La formule est la suivante :
Avec pref la pression de référence = 20.10-5Pa et p étant la pression efficace.
Ci-dessous un tableau représentant l’échelle des niveaux de pression sonore :
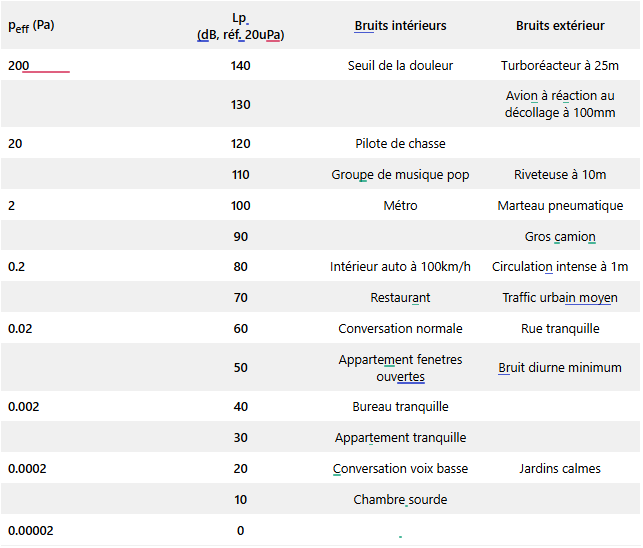
30dB + 30dB ne font pas 60dB ! et heureusement pour nos oreilles !
En effet, s’agissant d’une échelle logarithmique, les opérations doivent se faire en revenant aux pressions efficaces au carré donc pour sommer n niveaux sonores (ou intensité ou puissance) :
Il en découle donc que si on somme deux niveaux identiques :
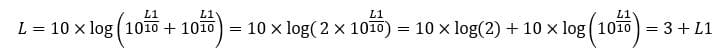
Pour calculer facilement et rapidement des sommes, différences et moyennes, vous pouvez utiliser le module Acouvapp ci-dessous :
Il s’agit de la vitesse à laquelle l’onde sonore circule. Dans l’air, la vitesse du son est calculée suivant :
c=(1.4 x P0 / ρ )1/2
avec
P0 : Pression atmosphérique en Pa
ρ: densité de l’air en kg/m3
La formule simplifiée est la suivante :
c=20.05 (T)(1/2)
avec T en Kelvin
La longueur d’onde (λ) est définie comme la distance pour un son pur parcouru durant une période T :
λ=c/f=c*T
Avec c, la célérité du son en m/s et f, la fréquence en Hz.
L’évolution temporelle d’un son peut être considérée comme un somme de sinus et cosinus évoluant avec différentes périodes temporelles.
Chacune de ces périodes (T) correspond à une fréquence (f=1/T). Si on prend l’exemple d’un son « pur », l’évolution temporelle présentera une ondulation avec une période temporelle donnée. Dans le domaine fréquentiel, ce même son sera donc représenté par un point à une seule fréquence (1/T).
Ils existent différentes représentations du spectre acoustique ou vibratoire. La plus utilisée est la représentation en octaves ou tiers d’octaves.
La largeur de la bande d’octave est délimitée par deux fréquences (appelées fréquences centrales) dont la fréquence supérieure est égale à deux fois la fréquence inférieure. La fréquence 1000Hz est définie comme la fréquence centrale « normalisée » d’où découlent toutes les autres fréquences centrales.
Afin d’affiner l’analyse spectrale, la représentation en tiers d’octave est souvent utilisée. Trois tiers d’octaves forment une octave. La relation entre deux tiers d’octave adjacents est avec .
Le tableau ci-dessous présente la liste des octaves et les tiers d’octaves :


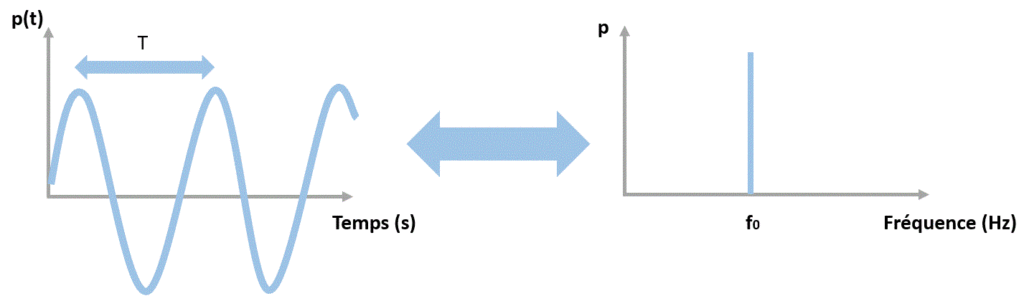
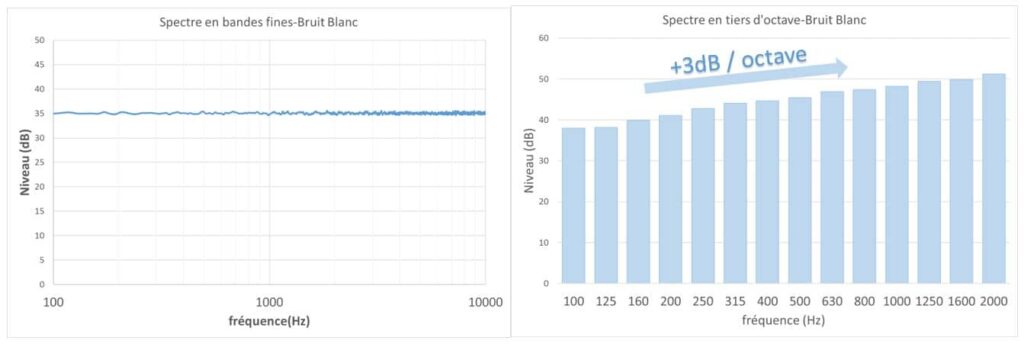
Il s’agit d’un son dont l’amplitude du spectre en bandes fines décroit de 3dB lorsque la fréquence double. Par contre, en tiers d’octave ou en octave, l’allure du spectre est constante (somme énergétique entre les bandes d’octaves et de tiers d’octaves).
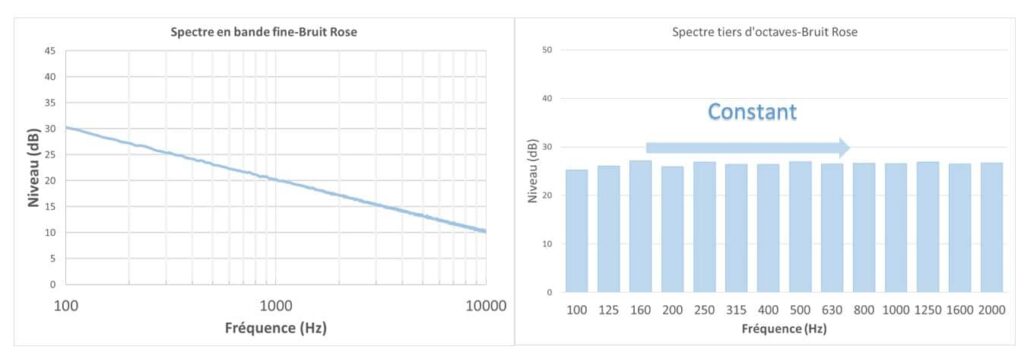
Il s’agit d’un son dont l’amplitude du spectre en bandes fines est stable lorsque la fréquence double. Par contre, en tiers d’octave ou en octave, l’amplitude du spectre augmente de 3dB par octave (somme énergétique entre les bandes d’octaves et de tiers d’octaves).
Cette définition est trop longue pour l’écrire ici, alors rdv sur la page puissance acoustique !
Ils existent deux sortes de pondérations : les pondérations fréquentielles et les pondérations temporelles.
Les pondérations fréquentielles les plus utilisées sont les suivantes :
Les pondérations fréquentielles s’ajoutent au niveau de pression acoustique pour chaque tiers d’octave ou octave (avec comme unité dB ou dBLin).
Les pondérations temporelles les plus utilisées sont :
Chacune possède une durée d’intégration qui lui est propre (moyenne exponentielle), soit respectivement, 35ms, 125ms et 1s. Comme indiqué, le choix de l’une des pondérations, dépendra du type de bruit à analyser (bruit court, long ou impulsionnelle).
Vous souhaitez passer d’une pondération A à C ou Lin à A, testez le module de Acouvapp sur le calcul de la pondération acoustique.
Le temps de réverbération est la durée de prolongation d’un son après l’interruption de la source sonore, du fait des multiples réflexions sur les parois d’un local.
Il est exprimé en seconde et représente le temps nécessaire pour que le niveau de pression acoustique diminue de 60 dB.
Les pondérations fréquentielles les plus utilisées sont les suivantes :
Le graphique ci-dessous présente une illustration de la détermination du temps de réverbération
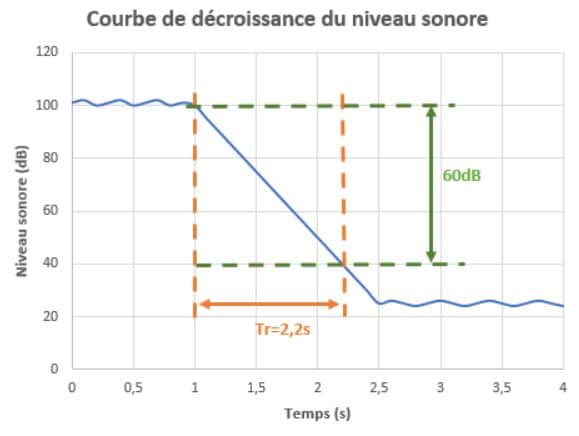
Le temps de réverbération dépend principalement :
Une mesure acoustique peut être réalisée avec différentes sources telles qu’un ballon qui éclate (méthode impulsionnelle) ou une source omnidirectionnelle (méthode de bruit interrompu). Plusieurs emplacements de microphones et de sources sont nécessaires lors de la mesure. Les normes 3382-1 à 3 décrivent les méthodes de mesures en fonction du type de salle.
Cette définition est trop longue pour l’écrire ici, alors rdv sur la page raideur dynamique des matériaux !
L’isolement acoustique est la capacité d’un matériau ou d’un système à limiter la transmission du bruit d’une pièce à une autre.
L’isolement R est défini en dB et plus il est élevé plus la paroi est performante. R est défini par la formule suivante :
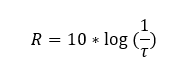
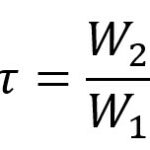
Plusieurs indices existent pour définir l’isolement, et il est vrai qu’on peut s’y perdre (R, Rw, Ra, R’…).
Pour y voir plus clair dans les indices, lire notre article : Indices et cie
De manière générale, une paroi est testée dans une double chambre réverbérante dans lesquelles (en laboratoire), on mesure les niveaux sonores avec des microphones en plusieurs positions puis l’indice d’affaiblissement est calculée en effectuant la différence des niveaux sonores (L2 – L1) par bandes de tiers d’octaves (ou octaves ou bandes fines) corrigés de l’aire d’absorption d’équivalente de la salle de réception et de la surface de l’élément à tester.
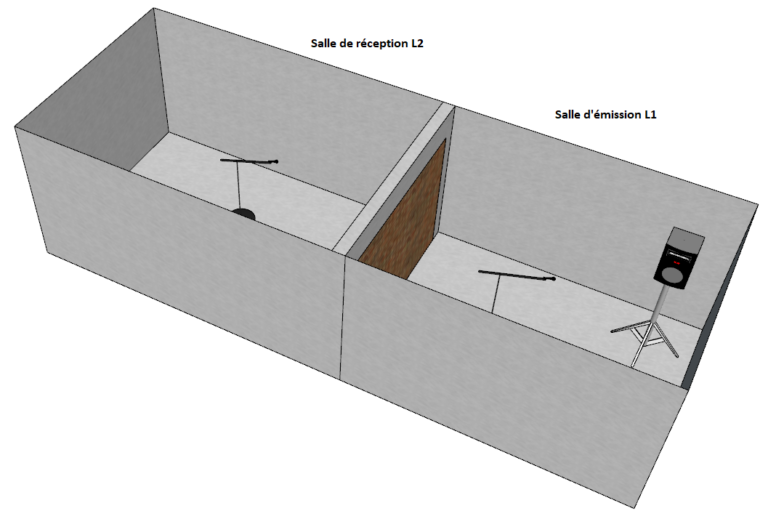
L’indice d’affaiblissement est présenté généralement en spectres de tiers d’octaves accompagnés des indices globaux Rw (indice d’affaiblissement pondéré) , Rw+C et Rw+Ctr, C et Ctr étant des termes d’adaptation à un spectre donné (C principalement pour une utilisation d’isolement aux bruits intérieurs et Ctr pour des isolements aux bruits extérieurs). Ces indices sont calculés suivant la norme ISO 717.
L’indice d’affaiblissement est fourni principalement sur la gamme de fréquence de 100Hz à 5000Hz mais il possible de mesurer à partir 50Hz (basses fréquences).
Les plots antivibratiles sont utilisés pour réduire la vibration sur une structure provenant d’un équipement. Différentes technologies existent tels que les plots élastomères, métalliques (ressorts),… En fonction de l’application et des contraintes (encombrement, raideur, amortissement, tenue à la température, durée de vie,…) , certaines technologies seront privilégiées.
Les plots agissent principalement comme des filtres de vibration, par conséquent ils seront efficaces sur une gamme de fréquence déterminée.
Cette fréquence dépendra principalement de la raideur du plot (K, rapport de la force et du déplacement) et de la masse suspendue (M).
Ces deux paramètres vont permettre de calculer la transmissibilité du plot, c’est-à-dire, le rapport entre la vibration en aval et la vibration en amont. Cette transmissibilité est caractérisée par plusieurs zones fréquentielles distinctes (voir graphique ci-dessous avec f la fréquence).

Comme précisé dans l’analyse du graphique ci-dessus, lors du dimensionnement d’un plot, l’objectif est de positionner la fréquence d’excitation de l’équipement dans la zone de réduction de vibration (zone verte). Une étude vibratoire est nécessaire pour dimensionner correctement les plots de suspension.
Plusieurs indices existent pour définir l’isolement, et il est vrai qu’on peut s’y perdre (R, Rw, Ra, R’…).
Pour y voir plus clair dans les indices, lire notre article : Indices et cie
De manière générale, une paroi est testée dans une double chambre réverbérante dans lesquelles (en laboratoire), on mesure les niveaux sonores avec des microphones en plusieurs positions puis l’indice d’affaiblissement est calculée en effectuant la différence des niveaux sonores (L2 – L1) par bandes de tiers d’octaves (ou octaves ou bandes fines) corrigés de l’aire d’absorption d’équivalente de la salle de réception et de la surface de l’élément à tester.

L’indice d’affaiblissement est présenté généralement en spectres de tiers d’octaves accompagnés des indices globaux Rw (indice d’affaiblissement pondéré) , Rw+C et Rw+Ctr, C et Ctr étant des termes d’adaptation à un spectre donné (C principalement pour une utilisation d’isolement aux bruits intérieurs et Ctr pour des isolements aux bruits extérieurs). Ces indices sont calculés suivant la norme ISO 717.
L’indice d’affaiblissement est fourni principalement sur la gamme de fréquence de 100Hz à 5000Hz mais il possible de mesurer à partir 50Hz (basses fréquences).